Pola figur płaskich |
|---|
ProstokątProstokąt ma cztery kąty proste i dwie pary boków równoległych. 
\[ \huge P = a \cdot b \] gdzie \( a \) i \( b \) to długość boków. |
KwadratKwadrat ma cztery kąty proste, wszystkie boki równej długości i dwie pary boków równoległych. 
\[ \huge P = a^2\] gdzie \( a \) to długość boku. Każdy kwadrat jest prostokątem bo ma cztery kąty proste. Nie każdy prostokąt jest kwadratem bo nie każdy prostokąt ma wszystkie boki równej długości. |
TrójkątKażdy trójkąt ma trzy boki i trzy wysokości. Licząc pole zawsze musimy wybrać parę wysokość-bok, między którymi jest kąt prosty. 
\[ \huge P = \frac{1}{2} \cdot a \cdot h\] gdzie \( a \) to podstawa, \( h \) to padająca na nią wysokość. Pamiętaj też, że wzór możemy zapisać w postaci ułamka: \[ \huge P = \frac{a \cdot h}{2}\] Nie ważne, której wysokości użyjesz, zawsze wynik wyjdzie ten sam. Możemy zapisać wzór dla boku b, używając indeksów dolnych. 
\[ \huge P = \frac{1}{2} \cdot b \cdot h_b\] gdzie \( b \) to podstawa, \( h_b \) to padająca na bok \( b \). Identycznie wyglądałby wzór gdybyśmy użyli boku \( c \). Podsumowójąc: \[ \textcolor{black}{P = \frac{a \cdot h_a}{2}= \frac{b \cdot h_b}{2}= \frac{c \cdot h_c}{2} }\] |
RównoległobokKażdy równoległobok ma dwie wysokości. Licząc pole zawsze musimy wybrać parę wysokość-bok, między którymi jest kąt prosty. 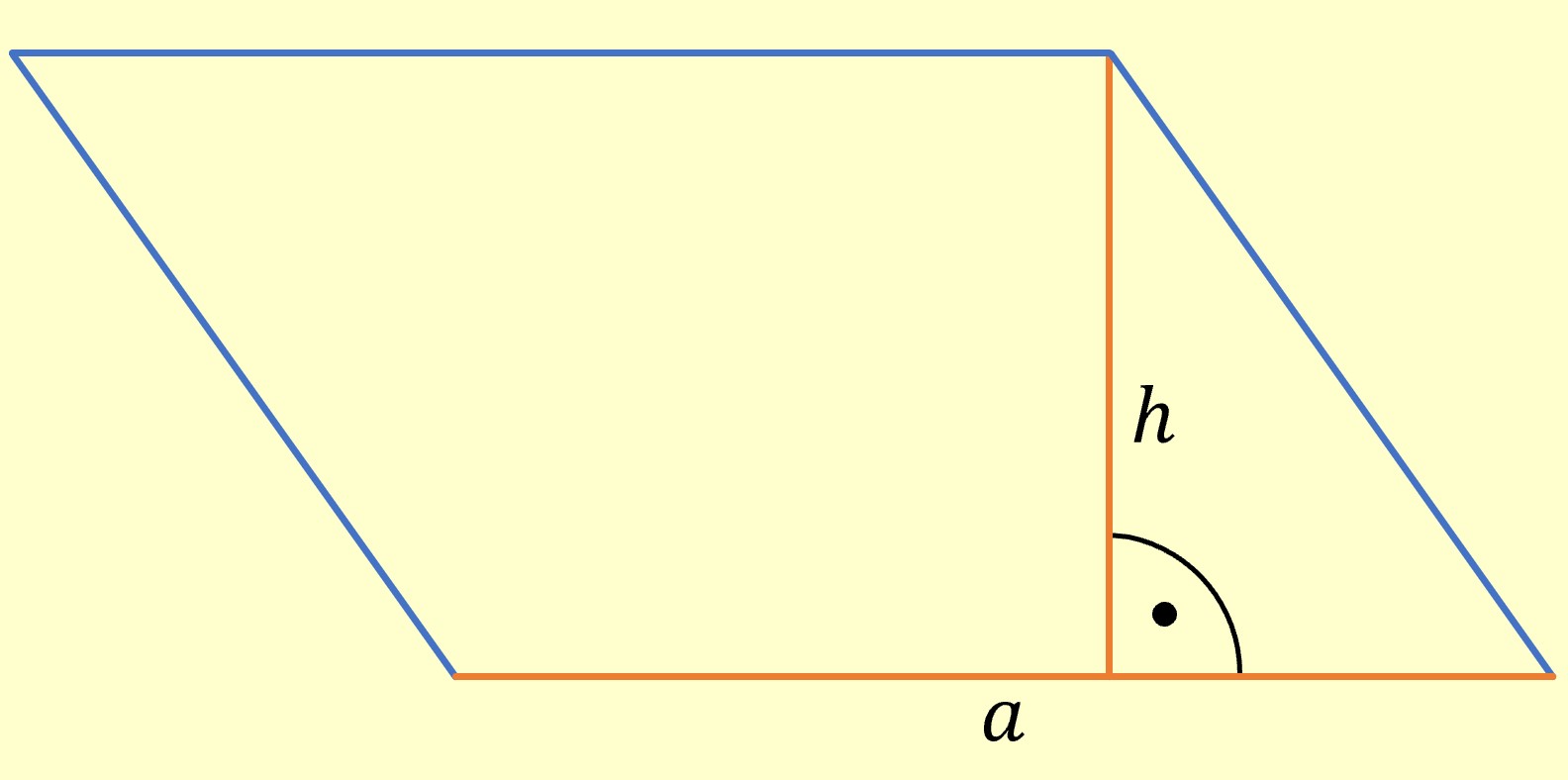
\[ \huge P = a \cdot h\] gdzie \( a \) to podstawa, \( h \) to padająca na nią wysokość. Tak jak w trójkącie, możemy napisać wzór używając drugiej wysokości. 
\[ \huge P = b \cdot h_b\] gdzie \( b \) to podstawa, \( h_b \) to padająca na bok \( b \). Podsumowójąc: \[ \textcolor{black}{P = a \cdot h_a = b \cdot h_b }\] |
RombRomb to szczególny przypadek, gdzie używamy przekątnych, zamiast długości boków. 
\[ \huge P = \frac{e \cdot f}{2}\] gdzie \( e \) i \( f \) to przekątne rombu. Ponieważ romb jest też równoległobokiem, więc moglibyśmy też użyć wzór na pole równoległoboku. 
\[ \huge P = b \cdot h_b\] gdzie \( b \) to podstawa, \( h_b \) to padająca na bok \( b \). Podsumowójąc: \[ \textcolor{black}{P = \frac{e \cdot f}{2} = a \cdot h_a}\] |
TrapezW trapezie mamy tylko jedną wysokość, za to używamy obu podstaw. 
\[ \huge P = \frac{a + b}{2} \cdot h\] gdzie \( a \) i \( b \) to podstawy trapezu, \( h \) to wysokość trapezu. |