Wahadło matematyczne |
||||||
|---|---|---|---|---|---|---|
WprowadzenieWahadło matematyczne to uproszczony model wahadła fizycznego, który dobrze opisuje zachowanie ciężarka kołyszącego się na lince. Zakładamy, że linka jest nierozciągliwa i nieważka, a w praktyce:
Kolejnym założeniem jest, że wahadło zostało wychylone o mały kąt, czyli mniejszy niż 15-20 stopni. Dla małego kąta możemy pominąć jego wpływ na okres. Dla większych kątów uproszczony wzór na okres przestaje dobrze działać. 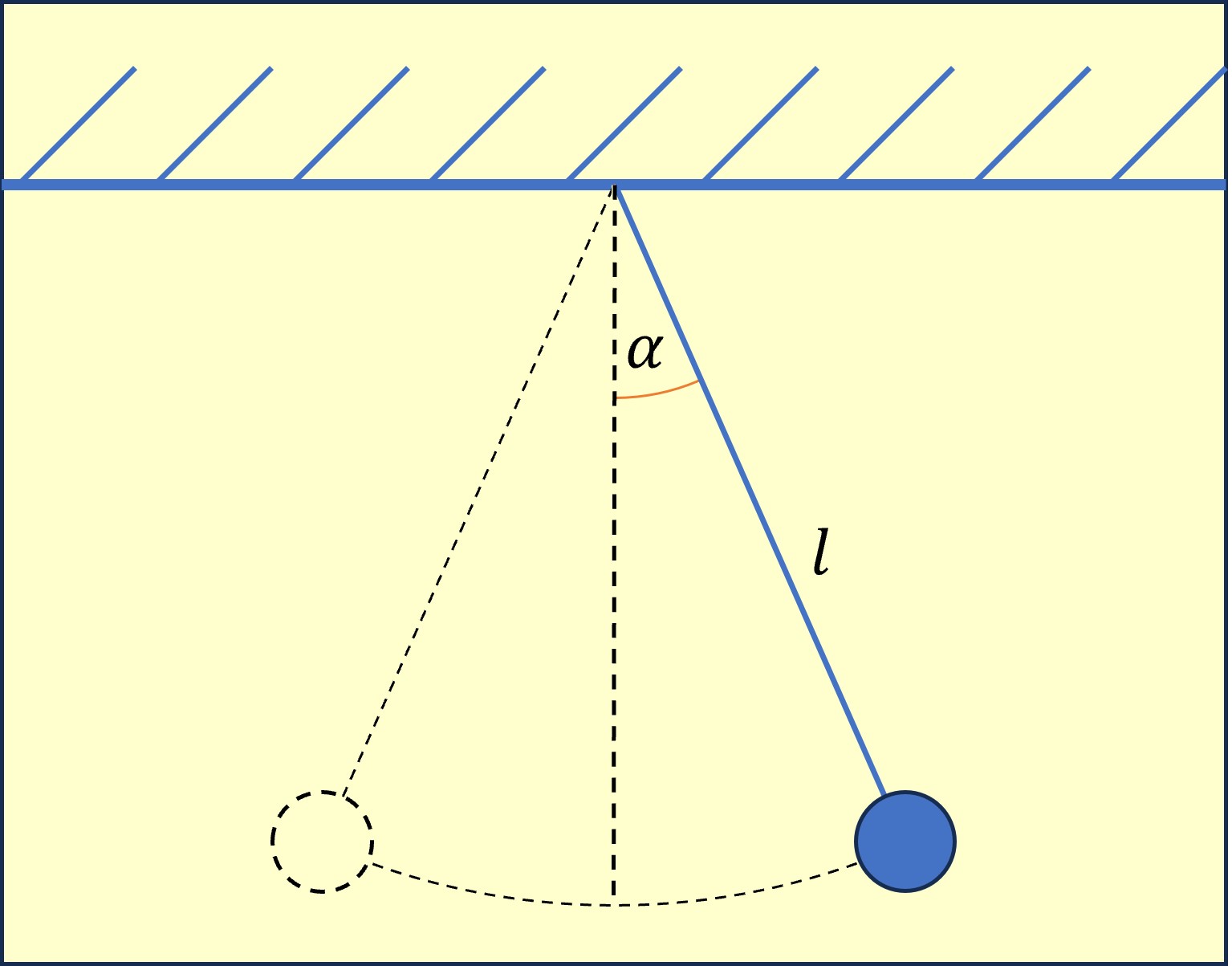
|
||||||
Okres wahadła matematycznegoOkres, czyli czas całego wahnięcia. Tam i z powrotem, całe, pełne wahnięcie. Ważne, że ciężarek musi wrócić dokładnie do tego samego stanu. Nie tylko do tego samego miejsca, ale też, potocznie mówiąc, tego samego kierunku (a dokładnie tego samego zwrotu wektora prędkości). Na przykładzie zdarzą się cztery sytuacje:
I tak w kółko. Nieważne, który moment wybierzemy, żeby mierzyć okres, ważne, żebyśmy mierzyli czas od tego samego stanu do tego samego stanu. Czas okresu wahadła matematycznego, w przypadku małych wychyleń, można obliczyć za pomocą wzoru: \( T = 2\pi \sqrt{\frac{l}{g}} \), gdzie \( T \) to czas jednego pełnego wahnięcia, \( l \) to długość linki, a \( g \) to przyspieszenie grawitacyjne. Od czego zależy, a od czego nie zależy okres wahadła?
|
||||||
Wahadło sekundoweWahadło sekundowe to wahadło, którego okres wynosi jedną sekundę, czyli \( T = 1s \). Aby obliczyć jego długość, musimy przekształcić wzór na okres, by wyliczyć długość. \( T = 2\pi \sqrt{\frac{l}{g}} \) \( T^2 = (2\pi)^2 \frac{l}{g} \) \( g \cdot T^2 = 4\pi^2 \cdot l \) \( \frac{g \cdot T^2}{4\pi^2} = l \) \( l = \frac{g \cdot T^2}{4\pi^2} \) Podstawiamy wartości liczbowe: \( l = \frac{9,81 \cdot (1)^2 }{4\pi^2} \) \( l = \frac{9,81}{4 \cdot \pi^2} \) \( l \approx 0,248 \, \text{m} \) Długość wahadła, dla którego okres wynosi 1 sekundę, wynosi około 0,248 m. |