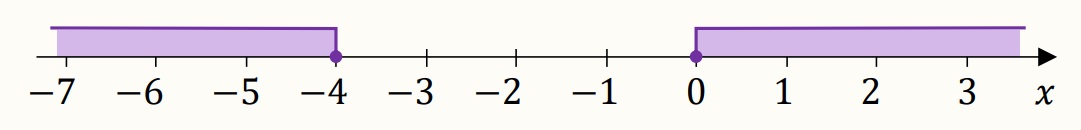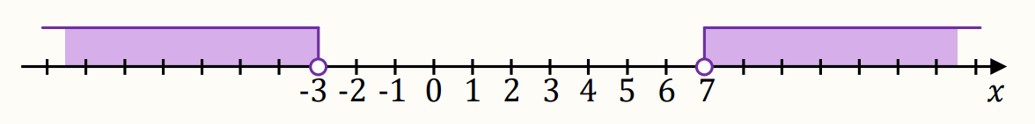Wskazówka

Odczytajmy nierówności z treści zadania:
\[ x \le -4 \qquad \lor \qquad x \ge 0 \]
Ponieważ mamy \( \lor \) (lub), to znaczy że w nierówności z wartością bezwzględną musi być \( \ge \). Dlatego musimy sprawdzć tylko odpowiedzi C i D.

Sprawdzając odpowiedź C zacznijmy od rozpisania dwóch możliwości: \[\left\vert x+2 \right\vert \ge 2 \] \[x+2 \ge 2 \qquad \lor \qquad x+2 \:\boxed{\phantom{\le}}\:\boxed{\phantom{-2}}\] \[x \ge 0 \qquad \lor \qquad x \:\boxed{\phantom{\le}}\:\boxed{\phantom{-4}}\] Teraz musisz sprawdzić, czy obie nierówności się zgadzają, lewa i prawa. Jeśli tak, to dobra odpowiedź. Jeśli nie, sprawdzasz odpowiedź D.

Rozwiązanie

Ponieważ mamy \( \lor \) (lub), to znaczy że w nierówności z wartością bezwzględną musi być \( \ge \). Dlatego musimy sprawdzć tylko odpowiedzi C i D.

Sprawdzamy odpowiedź C: \[\left\vert x+2 \right\vert \ge 2 \] \[x+2 \ge 2 \qquad \lor \qquad x+2 \le-2\] \[x \ge 0 \qquad \lor \qquad x \le-4\] Lewa strona się zgadza, prawa też. Czyli to dobra odpowiedź.

Wskazówka

Odczytajmy nierówności z treści zadania:
\[ x \le -2 \qquad \lor \qquad x \ge 5 \]
Ponieważ mamy \( \lor \) (lub), to znaczy że w nierówności z wartością bezwzględną musi być \( \ge \). Dlatego musimy sprawdzć tylko odpowiedzi A i B.

Sprawdzając odpowiedź A zacznijmy od rozpisania dwóch możliwości: \[\left\lvert x-3{,}5 \right\rvert \ge 1{,}5\] \[x-3{,}5 \ge 1{,}5 \qquad \lor \qquad x-3{,}5 \:\boxed{\phantom{\le}}\:\boxed{\phantom{-1{,}5}}\] \[x \ge 5 \qquad \lor \qquad x \:\boxed{\phantom{\le}}\:\boxed{\phantom{2}}\] Teraz musisz sprawdzić, czy obie nierówności się zgadzają, lewa i prawa. Jeśli tak, to dobra odpowiedź. Jeśli nie, sprawdzasz odpowiedź B.

Rozwiązanie

Ponieważ mamy \( \lor \) (lub), to znaczy że w nierówności z wartością bezwzględną musi być \( \ge \). Dlatego musimy sprawdzć tylko odpowiedzi A i B.

Sprawdzamy odpowiedź A: \[\left\lvert x-3{,}5 \right\rvert \ge 1{,}5\] \[x-3{,}5 \ge 1{,}5 \qquad \lor \qquad x-3{,}5 \le -1{,}5\] \[x \ge 5 \qquad \lor \qquad x \le 2\] Lewa strona się zgadza, prawa nie. Czyli to zła odpowiedź.

Sprawdzamy odpowiedź B: \[\left\lvert x-1{,}5 \right\rvert \ge 3{,}5\] \[x-1{,}5 \ge 3{,}5 \qquad \lor \qquad x-1{,}5 \le -3{,}5\] \[x \ge 5 \qquad \lor \qquad x \le -2\] Lewa strona się zgadza, prawa też. Czyli to dobra odpowiedź.

Wskazówka

Rozpiszmy dwie możliwości: \[\left\lvert x+5 \right\rvert < 15\] \[x+5 < 15 \qquad \land \qquad x+5 \: \boxed{\phantom{>}} \:\boxed{\phantom{-15}}\] \[x < \boxed{\phantom{10}} \qquad \land \qquad x \:\boxed{\phantom{>}}\:\boxed{\phantom{-20}}\]

Jakie liczby dodatnie są większe od \( \boxed{\phantom{-20}} \) i mniejsze od \(\boxed{\phantom{10}} \) ? Ile ich jest?

Rozwiązanie

Liczby całkowite należące do tego przedziału to: \( 1 \), \( 2 \) ... \(8 \), \( 9 \), czyli mamy \( 9 \) liczb całkowitych dodatnich.

Wskazówka

Nierówności z wartością bezwzględną zawsze mają dwie możliwości, "nieodwróconą" i "odwróconą: \[\left\vert x-5\right\vert <2 \] \[x-5<2\qquad \land\qquad x-5 \:\boxed{\phantom{>}}\:\boxed{\phantom{-2}}\] \[x<7\qquad \land\qquad x \:\boxed{\phantom{>}}\:\boxed{\phantom{3}}\] Gdy mamy już obie nierówności, znajdź właściwą odpowiedź.

Rozwiązanie

Wskazówka

Odczytajmy nierówności z treści zadania:
\[ x >-3 \qquad \land \qquad x <7 \]
Ponieważ mamy \( \land \) (i), to znaczy że w nierówności z wartością bezwzględną musi być \( < \). Dlatego musimy sprawdzć tylko odpowiedzi A i C.

Sprawdzając odpowiedź A zacznijmy od rozpisania dwóch możliwości: \[\left\vert x-2\right\vert <5 \] \[x-2 <5 \qquad \land \qquad x-2 \:\boxed{\phantom{>}}\:\boxed{\phantom{-5}}\] \[x<7 \qquad \land \qquad x \:\boxed{\phantom{>}}\:\boxed{\phantom{-3}}\] Teraz musisz sprawdzić, czy obie nierówności się zgadzają, lewa i prawa. Jeśli tak, to dobra odpowiedź. Jeśli nie, sprawdzasz odpowiedź C.

Rozwiązanie

Odczytajmy nierówności z treści zadania:
\[ x >-3 \qquad \land \qquad x <7 \]
Ponieważ mamy \( \land \) (i), to znaczy że w nierówności z wartością bezwzględną musi być \( < \). Dlatego musimy sprawdzć tylko odpowiedzi A i C.

Sprawdzamy odpowiedź A: \[\left\vert x-2\right\vert <5 \] \[x-2 <5 \qquad \land \qquad x-2 >-5\] \[x<7 \qquad \land \qquad x >-3\] Lewa strona się zgadza, prawa też. Czyli to dobra odpowiedź.

Wskazówka

Nierówności z wartością bezwzględną zawsze mają dwie możliwości, "nieodwróconą" i "odwróconą: \[\left\vert x-1\right\vert \ge 3 \] \[x-1\ge3\qquad \lor\qquad x-1 \:\boxed{\phantom{\le}}\:\boxed{\phantom{-3}}\] \[x\ge4\qquad \lor\qquad x \:\boxed{\phantom{\le}}\:\boxed{\phantom{-2}}\] Gdy mamy już obie nierówności, znajdź właściwą odpowiedź. Pamiętaj, że \(\ge\) i \(\le\) oznaczamy zamalowanym kółeczkiem a \(>\) i \(<\) niezamalowanym.

Rozwiązanie

\[\left\vert x-1\right\vert \ge 3 \] \[x-1\ge3\qquad \lor\qquad x-1 \le-3\] \[x\ge4\qquad \lor\qquad x\le-2\]

Wskazówka

Rozpiszmy dwie możliwości: \[\left\lvert x+1 \right\rvert < 3\] \[x+1 < 3 \qquad \land \qquad x+1 \: \boxed{\phantom{>}} \:\boxed{\phantom{-3}}\] \[x < \boxed{\phantom{2}} \qquad \land \qquad x \:\boxed{\phantom{>}}\:\boxed{\phantom{-4}}\]

Jakie liczby są większe od \( \boxed{\phantom{-4}} \) i mniejsze od \(\boxed{\phantom{2}} \) ? Ile ich jest?

Rozwiązanie

Liczby całkowite należące do tego przedziału to: \(-3 \), \(-2 \), \(-1 \), \(0 \), \(1 \), czyli mamy \(5 \) liczb całkowitych.

Wskazówka

Rozpiszmy dwie możliwości: \[\left\lvert x+4 \right\rvert = 7\] \[x+4 = 7 \qquad \lor \qquad x+4 =\:\boxed{\phantom{-7}}\] \[x = \boxed{\phantom{3}} \qquad \lor \qquad x =\:\boxed{\phantom{-11}}\]

Znaleźliśmy dwie odpowiedzi, czyli \( x_1=\boxed{\phantom{3}} \) i \( x_2=\boxed{\phantom{-11}} \). O co nas pytali w poleceniu?

Rozwiązanie

Rozpiszmy dwie możliwości: \[\left\lvert x+4 \right\rvert = 7\] \[x+4 = 7 \qquad \lor \qquad x+4 = -7\] \[x = 3 \qquad \lor \qquad x = -11\] Czyli: \( x_1=3 \) i \( x_2=-11 \). \[x_1 + x_2 = 3 + (-11) = -8 \]